கூம்பு வெட்டு எனவும் அழைக்கப்படும் கூம்பு வடிவ, எந்த வளைவு ஒரு விமானம் ஒன்றை ஒன்று வெட்டிக்கொள்ளும் பகுதிகள் உரிமை வட்ட கூம்பு தயாரிக்கப்பட்டது. கூம்புடன் தொடர்புடைய விமானத்தின் கோணத்தைப் பொறுத்து, குறுக்குவெட்டு என்பது ஒரு வட்டம், ஒரு நீள்வட்டம், ஒரு ஹைப்பர்போலா அல்லது ஒரு பரவளையமாகும். விமானம் உச்சத்தின் வழியாக (ஒரு புள்ளியை உருவாக்குகிறது) அல்லது உச்சத்தின் வழியாகவும், கூம்பின் மற்றொரு புள்ளி வழியாகவும் (ஒரு நேர் கோடு அல்லது இரண்டு குறுக்குவெட்டு நேர் கோடுகளை உருவாக்குகிறது) சந்திக்கும் போது சிறப்பு (சீரழிந்த) சந்திப்புகள் நிகழ்கின்றன. உருவத்தைப் பாருங்கள்.
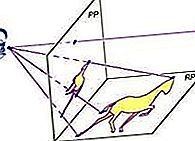
திட்ட வடிவியல்: திட்டவட்டமான கூம்பு பிரிவுகள்
கோனிக் பிரிவு கள் வலது வட்டக் கூம்பின் விமானப் பிரிவுகளாகக் கருதப்படலாம் (படத்தைப் பார்க்கவும்). தொடர்பாக
கோனிக் பிரிவுகளின் அடிப்படை விளக்கங்கள், ஆனால் பெயர்கள் அல்ல, பிளேடோ மற்றும் சினிடஸின் யூடோக்ஸஸ் ஆகிய இரண்டின் மாணவரான மெனெக்மஸ் (செழிப்பான சி. 350 பிசி) என்பதைக் காணலாம். "கிரேட் ஜியோமீட்டர்" என்று அழைக்கப்படும் பெர்காவின் அப்பல்லோனியஸ் (சி. கோனிக் பிரிவுகளைப் பற்றிய அப்பல்லோனியஸின் எட்டு தொகுதி கட்டுரை, கோனிக்ஸ், பண்டைய உலகின் மிகச் சிறந்த அறிவியல் படைப்புகளில் ஒன்றாகும்.
பகுப்பாய்வு வரையறை
கோனிக்ஸ் விமான வளைவுகள் என்றும் விவரிக்கப்படலாம், அவை ஒரு புள்ளியின் நகரும் பாதைகள் (லோகி), இதனால் ஒரு நிலையான புள்ளியிலிருந்து (கவனம்) ஒரு நிலையான வரியிலிருந்து (டைரக்ட்ரிக்ஸ்) தூரத்திற்கு அதன் தூரத்தின் விகிதம் ஒரு மாறிலி, என அழைக்கப்படுகிறது வளைவின் விசித்திரத்தன்மை. விசித்திரமானது பூஜ்ஜியமாக இருந்தால், வளைவு ஒரு வட்டம்; ஒன்றுக்கு சமமாக இருந்தால், ஒரு பரவளையம்; ஒன்றுக்கு குறைவாக இருந்தால், ஒரு நீள்வட்டம்; ஒன்றுக்கு மேற்பட்டதாக இருந்தால், ஒரு ஹைப்பர்போலா. உருவத்தைப் பாருங்கள்.
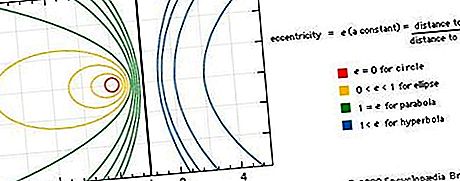
ஒவ்வொரு கோனிக் பகுதியும் அச்சு 2 + படிவத்தின் 2 டிகிரி பல்லுறுப்பு சமன்பாட்டின் வரைபடத்துடன் ஒத்திருக்கிறது, இதன் மூலம் 2 மற்றும் 2Cxy + 2Dx + 2Ey + F = 0, அங்கு x மற்றும் y மாறிகள் மற்றும் A, B, C, D, E, மற்றும் எஃப் என்பது குறிப்பிட்ட கோனிக் சார்ந்து இருக்கும் குணகங்களாகும். ஒருங்கிணைப்பு அச்சுகளின் பொருத்தமான தேர்வின் மூலம், எந்த கூம்புக்கான சமன்பாட்டை மூன்று எளிய r வடிவங்களில் ஒன்றாகக் குறைக்கலாம்: x 2 / a 2 + y 2 / b 2 = 1, x 2 / a 2 - y 2 / b 2 = 1, அல்லது y 2 = 2px, முறையே ஒரு நீள்வட்டம், ஒரு ஹைபர்போலா மற்றும் ஒரு பரவளையத்துடன் தொடர்புடையது. (ஒரு = பி உண்மையில் ஒரு வட்டம் இருக்கும் ஒரு நீள்வட்டம்.) வடிவியல் வளைவுகளின் இயற்கணித பகுப்பாய்விற்கான ஒருங்கிணைப்பு அமைப்புகளின் விரிவான பயன்பாடு ரெனே டெஸ்கார்ட்ஸுடன் (1596-1650) தோன்றியது. வடிவவியலின் வரலாறு: கார்ட்டீசியன் வடிவியல் பார்க்கவும்.
கிரேக்க தோற்றம்
கோனிக் பிரிவுகளின் ஆரம்பகால வரலாறு “கனசதுரத்தை இரட்டிப்பாக்குவது” என்ற பிரச்சினையுடன் இணைக்கப்பட்டுள்ளது. சைரனின் எரடோஸ்தீனஸின் கூற்றுப்படி (சி. 276-190 பிசி), டெலோஸ் மக்கள் அப்பல்லோவின் ஆரக்கிளை ஒரு பிளேக் (சி. அதே கன வடிவத்துடன். குழப்பமடைந்த டெலியன்ஸ் பிளேட்டோவிடம் ஆலோசித்தார், “ஆரக்கிள் என்பது கடவுள் இருமடங்கு அளவிலான ஒரு பலிபீடத்தை விரும்பினார் என்பதல்ல, ஆனால் பணியை அமைப்பதில் கிரேக்கர்கள் கணிதத்தை புறக்கணித்ததற்காகவும், அவமதிப்புக்காகவும் அவமானப்படுத்த விரும்பினார்” என்று கூறினார். வடிவவியலுக்கு. ” சியோஸின் ஹிப்போகிரேட்ஸ் (சி. 470-410 பிசி) முதன்முதலில் "டெலியன் சிக்கல்" ஒரு மற்றும் 2 அ (அந்தந்த பலிபீடங்களின் தொகுதிகள்) இடையே இரண்டு சராசரி விகிதாச்சாரங்களைக் கண்டுபிடிப்பதைக் குறைக்க முடியும் என்று கண்டுபிடித்தார்-அதாவது x மற்றும் y ஐ தீர்மானிப்பது: x = x: y = y: 2a. இது x 2 = ay, y 2 = 2ax, மற்றும் xy = 2a 2 ஆகிய இரண்டு சமன்பாடுகளையும் ஒரே நேரத்தில் தீர்க்க சமம், இது முறையே இரண்டு பரபோலாக்கள் மற்றும் ஒரு ஹைபர்போலாவுடன் ஒத்திருக்கிறது. பின்னர், ஆர்க்கிமிடிஸ் (சி. 290–211 பிசி) ஒரு கோளத்தை ஒரு குறிப்பிட்ட விகிதத்தைக் கொண்ட இரண்டு பிரிவுகளாகப் பிரிக்க கோனிக் பிரிவுகளை எவ்வாறு பயன்படுத்துவது என்பதைக் காட்டியது.
புரட்சியின் ஒரு பரவளையத்தின் அச்சுக்கு இணையான சூரியனை (உதாரணமாக, சூரியனில் இருந்து) கதிர்கள் (அதன் சமச்சீர் அச்சைப் பற்றி ஒரு பரவளையத்தை சுழற்றுவதன் மூலம் உற்பத்தி செய்யப்படுகின்றன) கவனம் செலுத்துகின்றன என்பதை டையோகிள்ஸ் (சி. 200 பிசி) வடிவியல் ரீதியாக நிரூபித்தது. ஆர்க்கிமிடிஸ் இந்த சொத்தை எதிரி கப்பல்களுக்கு தீ வைக்க பயன்படுத்தியதாக கூறப்படுகிறது. கான்ஸ்டான்டினோப்பிளில் உள்ள ஹாகியா சோபியா கதீட்ரலின் கட்டடக் கலைஞர்களில் ஒருவரான டிராலஸின் ஆன்டீமியஸ் (விளம்பரம் 537 இல் நிறைவு செய்யப்பட்டது), நீள்வட்டத்தின் குவிய பண்புகளை மேற்கோள் காட்டி, ஒரு பலிபீடம் நாள் முழுவதும் சூரிய ஒளியால் ஒளிரக்கூடும் என்பதை உறுதிசெய்கிறது.













