வரிசைமாற்றங்கள் மற்றும் சேர்க்கைகள், ஒரு தொகுப்பிலிருந்து பொருள்களைத் தேர்ந்தெடுப்பதற்கான பல்வேறு வழிகள், பொதுவாக மாற்றீடு இல்லாமல், துணைக்குழுக்களை உருவாக்குகின்றன. தேர்வின் வரிசை ஒரு காரணியாக இருக்கும்போது இந்த துணைக்குழுக்களின் வரிசைமாற்றம் என அழைக்கப்படுகிறது, ஒழுங்கு ஒரு காரணியாக இல்லாதபோது ஒரு சேர்க்கை. 17 ஆம் நூற்றாண்டில் பல விளையாட்டுகளுக்கு சாத்தியமான அனைத்து துணைக்குழுக்களின் எண்ணிக்கையையும் விரும்பிய துணைக்குழுக்களின் எண்ணிக்கையைக் கருத்தில் கொண்டு, பிரெஞ்சு கணிதவியலாளர்களான பிளேஸ் பாஸ்கல் மற்றும் பியர் டி ஃபெர்மட் ஆகியோர் கூட்டு மற்றும் நிகழ்தகவு கோட்பாட்டின் வளர்ச்சிக்கு உத்வேகம் அளித்தனர்.
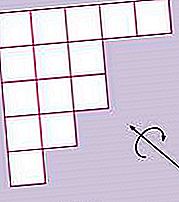
combinatorics: இரும குணகம்
n பொருள்களை ஒரு நேரத்தில் எடுக்கப்பட்ட n விஷயங்களின் வரிசைமாற்றம் என்று அழைக்கப்படுகிறது. வரிசைமாற்றங்களின் எண்ணிக்கை
வரிசைமாற்றங்கள் மற்றும் சேர்க்கைகளுக்கு இடையிலான கருத்துகள் மற்றும் வேறுபாடுகள் ஐந்து வேறுபட்ட பொருள்களிலிருந்து ஒரு ஜோடி பொருள்களைத் தேர்வுசெய்யக்கூடிய அனைத்து வெவ்வேறு வழிகளையும் ஆராய்வதன் மூலம் விளக்கலாம் A அதாவது A, B, C, D மற்றும் E போன்ற எழுத்துக்கள். தேர்ந்தெடுக்கப்பட்ட கடிதங்கள் மற்றும் தேர்வு வரிசை ஆகியவை கருதப்படுகின்றன, பின்னர் பின்வரும் 20 முடிவுகள் சாத்தியமாகும்:

இந்த 20 வெவ்வேறு தேர்வுகளில் ஒவ்வொன்றும் ஒரு வரிசைமாற்றம் என்று அழைக்கப்படுகிறது. குறிப்பாக, அவை ஒரே நேரத்தில் இரண்டு எடுக்கப்பட்ட ஐந்து பொருட்களின் வரிசைமாற்றங்கள் என்று அழைக்கப்படுகின்றன, மேலும் இதுபோன்ற வரிசைமாற்றங்களின் எண்ணிக்கை 5 பி 2 என்ற குறியீட்டால் குறிக்கப்படுகிறது, “5 வரிசை 2” ஐப் படியுங்கள். பொதுவாக, தேர்ந்தெடுப்பதற்கு n பொருள்கள் இருந்தால், மற்றும் ஒரு நேரத்தில் பொருள்களின் k ஐப் பயன்படுத்தி வரிசைமாற்றங்கள் (P) உருவாக்கப்பட வேண்டும் என்றால், சாத்தியமான வெவ்வேறு வரிசைமாற்றங்களின் எண்ணிக்கை n P k குறியீட்டால் குறிக்கப்படுகிறது. அதன் மதிப்பீட்டிற்கான ஒரு சூத்திரம் n P k = n! / (N - k)! வெளிப்பாடு n! —Rread “n காரணியாலானது” - 1 முதல் n வரையிலான அனைத்து நேர்மறை முழு எண்களும் ஒன்றாகப் பெருக்கப்பட வேண்டும் என்பதைக் குறிக்கிறது, மற்றும் 0! சமமாக வரையறுக்கப்படுகிறது 1. எடுத்துக்காட்டாக, இந்த சூத்திரத்தைப் பயன்படுத்தி, ஒரு நேரத்தில் இரண்டு எடுக்கப்பட்ட ஐந்து பொருட்களின் வரிசைமாற்றங்களின் எண்ணிக்கை

(K = n க்கு, n P k = n! இவ்வாறு, 5 பொருள்களுக்கு 5! = 120 ஏற்பாடுகள் உள்ளன.)
சேர்க்கைகளுக்கு, வரிசைப்படுத்தாமல் துணைக்குழுக்களை உருவாக்க n பொருள்களின் தொகுப்பிலிருந்து k பொருள்கள் தேர்ந்தெடுக்கப்படுகின்றன. முந்தைய வரிசைமாற்ற எடுத்துக்காட்டுடன் தொடர்புடைய கலவையுடன் ஒப்பிடுகையில், ஏபி மற்றும் பிஏ துணைக்குழுக்கள் இனி தனித்துவமான தேர்வுகள் அல்ல; இதுபோன்ற நிகழ்வுகளை நீக்குவதன் மூலம் 10 வெவ்வேறு துணைக்குழுக்கள் மட்டுமே உள்ளன - ஏபி, ஏசி, ஏடி, ஏஇ, கிமு, பிடி, பிஇ, சிடி, சிஇ மற்றும் டிஇ.
அத்தகைய துணைக்குழுக்களின் எண்ணிக்கை n C k ஆல் குறிக்கப்படுகிறது, “n தேர்வு k ஐ” படிக்கவும். சேர்க்கைகளுக்கு, k பொருள்களுக்கு k இருப்பதால்! ஏற்பாடுகள், கே உள்ளன! கே பொருள்களின் ஒவ்வொரு தேர்வுக்கும் பிரித்தறிய முடியாத வரிசைமாற்றங்கள்; எனவே வரிசைமாற்ற சூத்திரத்தை k ஆல் வகுக்கிறது! பின்வரும் சேர்க்கை சூத்திரத்தை அளிக்கிறது:
இது (n, k) இருமுனை குணகம் போன்றது (இருவகையான தேற்றத்தைப் பார்க்கவும்). எடுத்துக்காட்டாக, ஒரே நேரத்தில் இரண்டு எடுக்கப்பட்ட ஐந்து பொருட்களின் சேர்க்கைகளின் எண்ணிக்கை
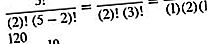
N P k மற்றும் n C k க்கான சூத்திரங்கள் எண்ணும் சூத்திரங்கள் என்று அழைக்கப்படுகின்றன, ஏனெனில் அவை அனைத்தையும் பட்டியலிடாமல் ஒரு குறிப்பிட்ட சூழ்நிலையில் சாத்தியமான வரிசைமாற்றங்கள் அல்லது சேர்க்கைகளின் எண்ணிக்கையை கணக்கிட பயன்படுத்தலாம்.